| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 알고리즘 #자료구조 #퀵소트 #정렬 #시간복잡도
- 타이젠
- PS #문제출제 #알고리즘 #곰곰이
- Problem Solving
- 뿌요뿌요2
- UCPC
- rounded corner
- Tizen
- 대회 후기
- 메이플스토리2
- 히노히에
- 콘솔게임
- 이산로그
- SUAPC #낙서장 #대회후기
- ui 그래픽스
- 낙서장
- 프로그래밍
- Dali
- C언어
- 곰곰이
- 뿌요뿌요
- Hinohie
- Today
- Total
히농의 잡합다식
제2회 임스의 메이플컵 출제 후기 본문
안녕하세요.
원래는 한동안 PS 를 접고 뒷방늙은이로 평화롭게 살고 있었는데,
메이플컵이 2회를 연다는 소식을 듣고, 메이플스토리2 유저로서 가만히 있을 수 없었습니다.
메컵콩 메이플스토리2 컨셉의 문제를 출제해도 된다는 허락을 받고, 몇 가지 문제를 제시했는데, 어쩌다보니 모두 채택되어서 3문제나 출제하게 되었습니다.
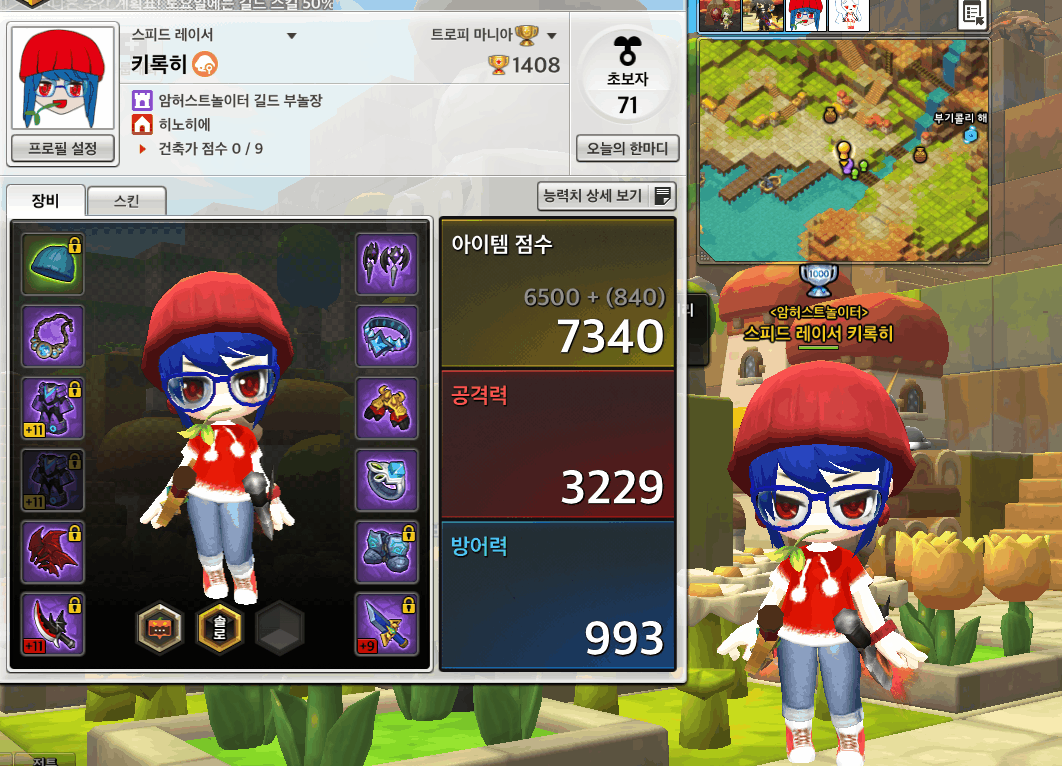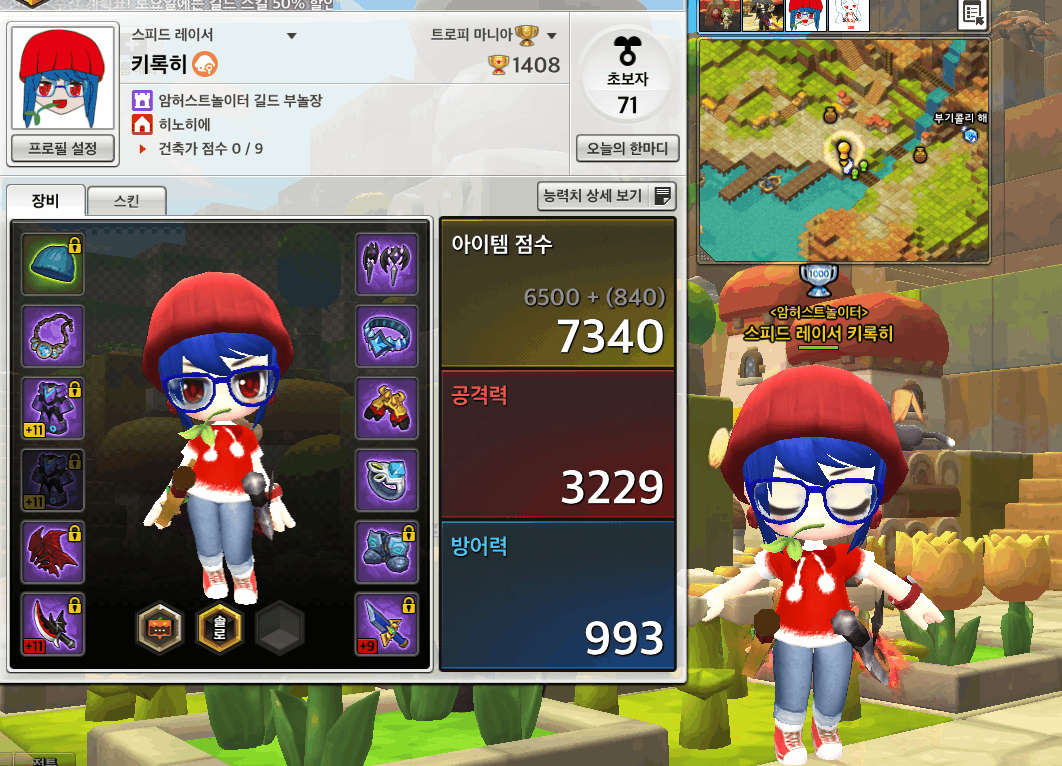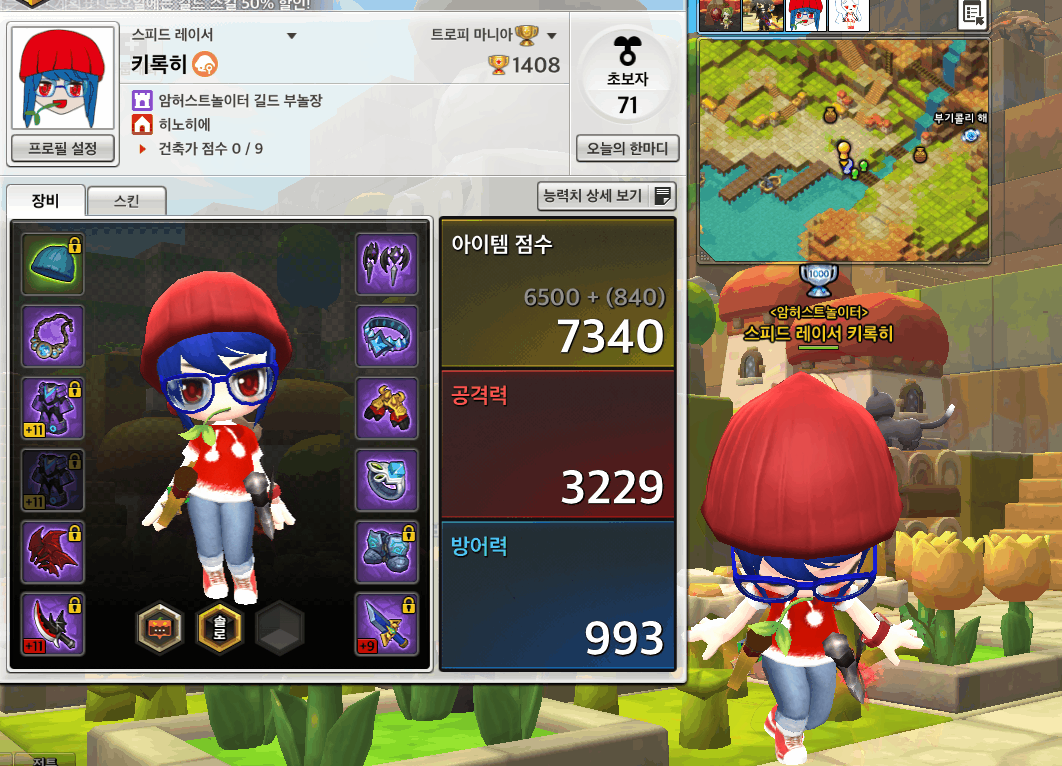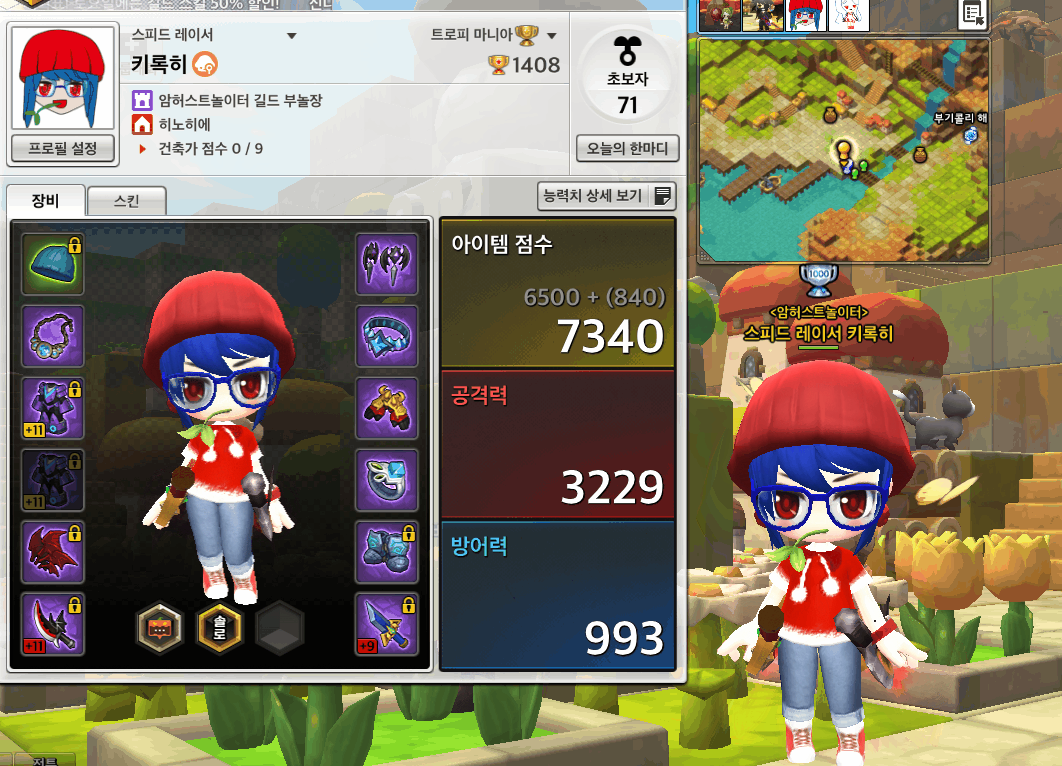
나름 인생의 1/10 넘게 투자한 게임이라서 애정을 가지고 있었고, 올해 25년 5월 29일을 기점으로 서비스종료가 예고되어있어, 지금이 아니면 관련 컨셉으로 문제를 더이상 출제할 수 없을 것 같았기에, 추모의 마음을 담아서 문제를 만들었습니다.
"파이널 서바이버 게임에서 1,000 회 우승하기" 라는 도전과제가 있었습니다. 보통 저같은 사람은 일 하면서 잠수를 타다가 가끔 생각나면 잠깐 움직이기 때문에 게임 참가 버튼 한번 눌러놓고 잠수를 탑니다.
이 게임에 참가해서 잠수를 탔을 때, 살아남을 확률이 얼마가 될지 궁금해서 만들었던 프로그램을 확장시켜, 문제로 만들었습니다.
기본적으로 꼭지점에 인접한 블록의 갯수만이 확률에 영향을 줍니다. 따라서 꼭지점에 인접한 블록 갯수가 최대가 되도록 서있는 것이 무조건 유리합니다.
그 다음은 확률을 계산하는 것인데, 이 문제를 잘 정리해보면 N 개중 4개를 선택했을 때, 내가 선택한 K 개가 포함될 확률을 구하는 것과 같습니다. N <= 64 이고 K 는 인접한 블록의 갯수 최대값 (1~4) 입니다. 64C4 <= 2^24 이기 때문에 합리적인 시간 내에 시뮬레이션을 통해서도 값을 계산할 수 있습니다.
적당한 노가다성 구현문제가 필요해서 만든 문제입니다. 초보자는 태생부터 남들보다 불리한 조건으로 사냥을 해야하는 직업입니다. 대신에 사용할 수 있는 스킬이 매우 적기 때문에 고민할 것도 없었습니다.
이 한정적인 스킬들을 사용해 보스를 뚜까팰 수 있는 가장 최적의 스킬 사이클이 무엇인지 계산하기 위해서 사용했던 프로그램을 확장시켜, 문제로 만들었습니다.
초보자 1인 에네르 캐슬 도전 영상에서 5시간 내내 보스봅을 사냥했던 기록도 있습니다. 흑흑...
시간, SP, 스트라이크 쿨타임, 박치키 쿨타임 총 4개의 변수에 대해서 4차원 DP table dp[601][101][3][8] 을 만들고, dp[t][s][b][c] 값은 최대 데미지로 정의한 뒤 DP 로 풀면 됩니다.
- dp[t][s][b][c] 에서 시작해, 다음과 같이 업데이트를 진행합니다.
- newT = t+1
- newS = min(s+1, 100);
- newB = max(b-1, 0);
- newC = max(c-1, 0);
- if(b == 2 || c == 7) { dp[newT][newS][newB][newC] <-- dp[t][s][b][c]; continue; } ///< 후딜레이 처리
- dp[newT][newS][newB][newC] <-- dp[t][s][b][c] + 100; ///< 평타
- dp[newT][min(newS + 7, 100)][newB][newC] <-- dp[t][s][b][c] + A; ///< 해머링
- if(newS >= 10 && b == 0) dp[newT][newS - 10][2][newC] <-- dp[t][s][b][c] + B; ///< 스트라이크
- if(newS >= 10 && c == 0) dp[newT][newS - 10][newB][7] <-- dp[t][s][b][c] + C; ///< 박치기
여기서 시간은 바로 직전 시간만 필요하기 때문에 메모리복잡도를 dp[2][101][3][8] 까지 줄일 수 있습니다만, 이런 최적화까지는 요구하지 않았습니다.
원래는 후 딜레이와 쿨타임이 실제 게임과 일치하는 0.5초 단위였고, 따라서 dp table 크기도 더 복잡했습니다. 하지만 초반부에 출제될 문제에서 굳이 지문의 복잡도를 높일 필요가 없다 생각해, 문제를 단순화시켜서 지금과 같은 모습이 되었습니다.
저의 얼이 담긴 문제입니다. 처음에 문제풀이 동아리 같은 것도 없고, 백준 사이트도 없었던 새싹 새내기 pichulia 가 2010년도에 구상한 문제입니다. 그 때 당시에는 N<=50 정도로, 커팅을 사용한 완전탐색을 상정한 문제였습니다.
만약에 제가 출제한 문제들로만 이루어진 PCPC 라는 이름의 대회가 열린다면 꼭 출제하고 싶었던 4개의 문제 중 하나입니다. 이렇게 세상에 공개되어서 너무 기쁘네요.
N <= 50 이던 시절 완전탐색으로 푸는 방법은 대략적으로 다음과 같습니다.
- 블록을 xyz 평면 위에 놓았다고 생각해보자. 각 블록을 xy, yz, zx 평면으로 최대한 밀어붙였다고 생각해도 겉넓이는 달라지지 않는다. 따라서 각 xy, yz, zx 평면에 블록을 어떻게 놓을 것인지 결정하면 된다.
- 우선 각 x,y,z 축에 블록을 몇 개씩 놓을 것인지 결정한다. 일반성을 잃지 않고, z <= y <= x 축 순으로 블록이 많다고 가정하면, z 축에는 최대 16개의 블록이 놓이게 된다. (실제로는 4개가 최대로 놓인다.)
- 이제 xz 평면, yz 평면에 블록을 얼마나 놓을 것인지를 재귀적으로 판단해서 추가한다.
- 이렇게 준비한 크기 z 짜리 수열 2개 (하나는 xz평면, 하나는 yz평면의 블록 정보를 나타낸다.) 가 주어졌을 때, 이를 활용해서 xy 평면에 블록을 어떻게 놓을지를 결정할 수 있다. 겉넓이 1 을 사용해서 추가할 수 있는 블록의 개수가 (x-1) * (y-1) 가지 결정되고, 이를 내림차순으로 정렬해서 겉넓이를 1씩 소모시킬 수 있다.
위와 같은 방법으로 완전탐색 풀이를 구현하고, 적절하게 컷팅하면 N <= 50 까지는 유의미한 시간 내에 답을 구할 수 있습니다.
위 설명을 토대로 구현한 코드
사실 2010년도에 짜놨던 정답 풀이는 전혀 다른 dp 식으로 풀었는데, 해석하는데 실패했기에 위와 같이 전혀 새로운 풀이를 떠올리게 되었습니다.
철저하게 암호화 되어있는 15년전 코드. 강산이 한 번 변했다.
위 코드들을 토대로 문제를 출제했다가 검수진으로부터 더 나은 Greedy 풀이법을 제안받았었습니다. 생각해보니 굳이 어렵게 생각할 필요가 없었습니다.
- 기본적으로 정답이 되는 형태는 xyz 꼴의 직육면체 형태와 비슷할 것이다.
- 직육면체 형태를 벗어나는 블록은 겉넓이를 넓힐 뿐.
- 우선 xyz < N <= xy(z+1) 을 만족하는 x, y, z 를 찾는다. x 와 y 가 고정되어있을 때, 이를 만족하는 z 를 O(1) 에 찾을 수 있다.
- 이후 z축으로 1층을 더 쌓아 올리되, 겉넓이가 최소가 되도록하는, 정사각형에 가까운 모습이 되는 것이 좋다.
- M = N - xyz 라고 했을 때, p*q <= M < p*(q+1) 을 만족하는 p, q 를 찾고, 이 때 p+q 값이 최소가 되어야하는 상황과 동치이다. 이 때 p,q 값 각각이 sqrt(M) 에 가까워야지 p+q 값이 최소인 것은 산술기하평균 부등식으로 증명할 수 있다.
- 위 상황에서, p <= x, q <= y 또는 p <= y, q <= x 조건을 만족해야한다.
- 위 일련의 과정은 M 이 결정되면 O(1) 이내에 계산이 가능하다.
- 가능한 x,y 값의 조합을 x = 1 ~ sqrt(N), y = x ~ N/x 범위 내에서 완전탐색한다.전체 시간복잡도는 O(N * (1 + 1/2 + 1/3 + .. + 1/sqrt(N)) 인데, 적당히 퉁쳐서 O(N log N) 이하라고 우길 수 있다.
- 유일한 예외인 z = 0 인 경우만 잘 처리한다.
- 자세한 증명은 생략....
위 풀이에 대한 반례가 될만한 상황은 사실 N 이 너무 작아서 직육면체 형태가 아닌 것이 더 최적일 수 있는 상황 뿐입니다.
다행히 완전탐색을 통해 구한 답과, 위 풀이로 구한 답이 일치하는 것을 확인했습니다.
생각보다 어려운 문제라고 생각해는데 모두들 잘 풀어줘서 의외라고 생각했습니다.
15년전의 저는 O(N^4) 이상의 정체불명의 풀이 밖에 떠올리지 못했는데, 이제는 O(N log N), 혹은 이보다 더 작은 시간복잡도도 떠올릴 수 있게 되었습니다. 그래서 저 개인적으로도 조금 성장했다는 기분도 들었습니다.
이제는 Problem Solving 을 하면서 취미활동을 하기에는 제가 너무 늙어버렸습니다. 게다가 이제 더이상 혼자 살고 있지 않으며, 평생을 책임져야하는 생명체도 여럿 생겼습니다. 따라서 이제 문제를 출제하고 검수하는 활동은 이번 대회 이후로 더 이상 할 수 없을 것이라 생각중입니다.
하지만..혹시 20여년 뒤에 은퇴같은 것을 하게 되어 여유가 생기면 또 다서 문제풀이의 세계에 뛰어들어서 뒷방늙은이 phase 2 로 살아갈지도 모릅니다. 그 때가 되면 세상은 또 어떻게 바뀌어 있을까요? 그때까지 제가 구상한 문제들을 출제할 수 있을까요? 모르겠네요.
그럼 이만. 바이바이 메콩!
'프로그래밍' 카테고리의 다른 글
| Tizen OS / DALi 에서 구현한 Corner Radius 설계도 (1/N) (0) | 2024.11.04 |
|---|---|
| 제 2회 곰곰컵 출제 후기 (GGANALi) (1) | 2022.11.27 |
| Tkinter 를 이용한 예금/적금 이자 비교 프로그램 코드 (2) | 2022.08.14 |
| 정수 자료형 퀵소트(quick sort) 의 상한선은 O(N log A) 이다. (0) | 2022.05.21 |
| SUAPC 2021 : 기지국 업그레이드 이미지 제작 후기 (1) | 2021.08.29 |




